Multivariate meta-analysis handles within-study dependence among effect sizes caused by the fact that multiple effect sizes were obtained from the same participants in the primary studies. This dependence could increase Type I error rate and lead to inaccurate estimates of study effects. However, multivariate meta-analysis is not popular in practice because it is difficult to computer the covariances among effect size, especially when the types of effect sizes are different. The package metavcov aims to provide a useful tool, metavcov (Lu 2021), for conducting multivariate meta-analysis with examples in R on how to perform multivariate meta-analysis of effect sizes. Effect sizes include correlation (r), mean difference (MD), standardized mean difference (SMD), log odds ratio (logOR), log risk ratio (logRR), and risk difference (RD). The package metavcov is listed under the section “Preparing for meta-analysis” in CRAN Task View: Meta-Analysis by Dewey (2021). {}
Introduction
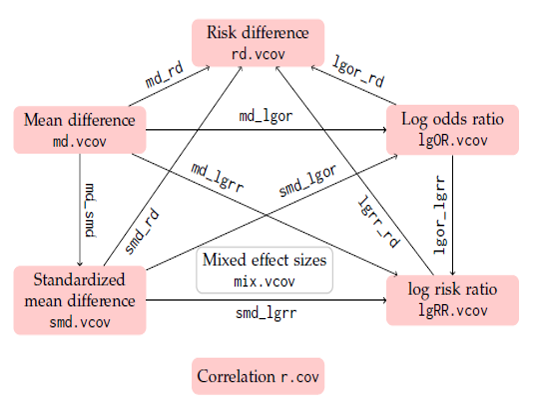
The R package metavcov facilitates multivariate meta-analysis via computing variance-covariance matrix among effect sizes including correlation (r, r.vcov()), mean difference (MD, md.vcov()), standardized mean difference (SMD, smd.vcov()), log odds ratio (logOR, lgOR.vcov()), log risk ratio (logRR, lgRR.vcov()), and risk difference (RD, rd.vcov()), as well as variance-covariance matrix among different types of effect sizes, such as covariance between log odds ratio and risk difference, lgor_rd(). All functions are shown in Figure 1.
Figure 1

Installation
Like many other R packages, the simplest way to obtain metavcov is to install it directly from CRAN via typing the following command in R console:
install.packages("metavcov", repos = "https://cran.us.r-project.org")For more details, see help(install.packages). Alternatively, users can download the package source from CRAN and type Unix commands:
ant source-cran
will create the R source code package directory-tree ./target/cran/metavcov/. To install metavcov in your default library, change to the directory ./target/cran/ and type
R CMD INSTALL --preclean --clean metavcov
Citation
To cite the R package metavcov (Lu 2021) in R (R Core Team 2020), users can run the following code in R console:
citation("metavcov")
> To cite metavcov in publications use:
>
> Lu M. (2021). Variance-Covariance Matrix for Multivariate
> Meta-Analysis, R package version 2.1.Users can run toBibtex(citation("metavcov")) for .bib file and citation("base") for citing the R software.
Quick Start
In this vignette, we will provide a general sense of the package. We will briefly go over the main functions and outputs using correlation effect sizes.
First, Let’s load the metavcov package:
library("metavcov")As a quick start, let’s use the data in Craft et al. (2003) (see Craft2003()) as an example, which examined the interrelationships between athletic performance and three subscales, cognitive anxiety, somatic anxiety, and self-concept from 18 studies. Since we have four outcomes, we have six (combn(4,2)) combinations of correlations among them, which are listed as C1-C6 in the dataset:
| Variable | Description |
|---|---|
| ID | ID for each study included |
| N | Sample size from each study included |
| gender | Gender |
| p_male | Percentage of male |
| C1 | Correlation coefficient between cognitive anxiety and somatic anxiety |
| C2 | Correlation coefficient between cognitive anxiety and self concept |
| C3 | Correlation coefficient between cognitive anxiety and athletic performance |
| C4 | Correlation coefficient between somatic anxiety and self concept |
| C5 | Correlation coefficient between somatic anxiety and athletic performance |
| C6 | Correlation coefficient between self concept and athletic performance |
Next, let’s use r.vcov() to compute the z scores and their variance-covariance matrix.
library("metavcov")
data(Craft2003)
#extract correlation from the dataset (craft)
corflat <- subset(Craft2003, select=C1:C6)
# transform correlations to z and compute variance-covariance matrix.
computvocv <- r.vcov(n = Craft2003$N, corflat = corflat, method = "average")
# name transformed z scores as an input
Input <- computvocv$ef
head(Input)
> C1 C2 C3 C4 C5 C6
> 1 0.2447741 -0.4236489 -0.3540925 -0.17166666 0.08017133 0.21317135
> 2 0.4476920 -0.4476920 -0.5229843 -0.08017133 0.17166666 -0.12058103
> 3 0.3428283 -0.1923372 -0.6776661 -0.14092558 -0.11044692 0.09024419
> 4 0.2152645 -0.6098195 -0.4611242 -0.41297996 -0.16755048 0.19337483
> 5 0.5100703 -0.3884231 -0.5493061 0.10033535 0.32054541 -0.17166666
> 6 0.8107431 -0.3768859 -0.9076450 -0.15114044 -0.42364893 0.36544375
# name variance-covariance matrix of trnasformed z scores as covars
covars <- computvocv$matrix.vcov
head(covars)
> [,1] [,2] [,3] [,4] [,5]
> [1,] 0.04761905 0.0003351688 0.002138113 -0.010579071 -0.013761771
> [2,] 0.04166667 0.0002979278 0.001900545 -0.009403618 -0.012232685
> [3,] 0.03703704 0.0002681350 0.001710490 -0.008463256 -0.011009417
> [4,] 0.09090909 0.0005745750 0.003665336 -0.018135549 -0.023591607
> [5,] 0.02380952 0.0001787567 0.001140327 -0.005642171 -0.007339611
> [6,] 0.04761905 0.0003351688 0.002138113 -0.010579071 -0.013761771
> [,6] [,7] [,8] [,9] [,10] [,11]
> [1,] -0.0011673589 0.04761905 0.003998742 0.02506561 0.002305253 -0.013540829
> [2,] -0.0010376523 0.04166667 0.003554437 0.02228054 0.002049114 -0.012036292
> [3,] -0.0009338871 0.03703704 0.003198993 0.02005248 0.001844203 -0.010832663
> [4,] -0.0020011867 0.09090909 0.006854986 0.04296961 0.003951863 -0.023212849
> [5,] -0.0006225914 0.02380952 0.002132662 0.01336832 0.001229468 -0.007221775
> [6,] -0.0011673589 0.04761905 0.003998742 0.02506561 0.002305253 -0.013540829
> [,12] [,13] [,14] [,15] [,16] [,17]
> [1,] 0.04761905 0.001963746 0.02512404 -0.010480026 0.04761905 0.005879878
> [2,] 0.04166667 0.001745552 0.02233248 -0.009315578 0.04166667 0.005226558
> [3,] 0.03703704 0.001570997 0.02009923 -0.008384021 0.03703704 0.004703902
> [4,] 0.09090909 0.003366422 0.04306978 -0.017965758 0.09090909 0.010079791
> [5,] 0.02380952 0.001047331 0.01339949 -0.005589347 0.02380952 0.003135935
> [6,] 0.04761905 0.001963746 0.02512404 -0.010480026 0.04761905 0.005879878
> [,18] [,19] [,20] [,21]
> [1,] -0.0017802532 0.04761905 -0.002948570 0.04761905
> [2,] -0.0015824473 0.04166667 -0.002620951 0.04166667
> [3,] -0.0014242026 0.03703704 -0.002358856 0.03703704
> [4,] -0.0030518626 0.09090909 -0.005054692 0.09090909
> [5,] -0.0009494684 0.02380952 -0.001572571 0.02380952
> [6,] -0.0017802532 0.04761905 -0.002948570 0.04761905Finally, let’s use the package mvmeta to complete this multivariate meta analysis.
library(mvmeta)
mvmeta_RE <- summary(mvmeta(cbind(C1, C2, C3, C4, C5, C6),
S = covars, data = Input, method = "reml"))
mvmeta_RE
> Call: mvmeta(formula = cbind(C1, C2, C3, C4, C5, C6) ~ 1, S = covars,
> data = Input, method = "reml")
>
> Multivariate random-effects meta-analysis
> Dimension: 6
> Estimation method: REML
>
> Fixed-effects coefficients
> Estimate Std. Error z Pr(>|z|) 95%ci.lb 95%ci.ub
> C1 0.5033 0.0637 7.9016 0.0000 0.3784 0.6281 ***
> C2 -0.2666 0.0421 -6.3404 0.0000 -0.3491 -0.1842 ***
> C3 -0.3516 0.0810 -4.3394 0.0000 -0.5104 -0.1928 ***
> C4 -0.0246 0.0543 -0.4538 0.6499 -0.1311 0.0818
> C5 -0.0004 0.0516 -0.0078 0.9938 -0.1014 0.1006
> C6 0.0328 0.0661 0.4961 0.6198 -0.0967 0.1623
> ---
> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
>
> Between-study random-effects (co)variance components
> Structure: General positive-definite
> Std. Dev Corr
> C1 0.2116 C1 C2 C3 C4 C5
> C2 0.1075 -0.3361
> C3 0.2896 -0.2672 -0.1089
> C4 0.1741 -0.3114 -0.7897 0.3173
> C5 0.1620 -0.3772 -0.7222 0.4911 0.9810
> C6 0.2266 0.8901 0.1085 -0.4630 -0.6933 -0.7562
>
> Multivariate Cochran Q-test for heterogeneity:
> Q = 349.8594 (df = 102), p-value = 0.0000
> I-square statistic = 70.8%
>
> 18 studies, 108 observations, 6 fixed and 21 random-effects parameters
> logLik AIC BIC
> 0.2746 53.4508 124.3251You could use the following code for meta-regression, but there is no significant difference in gender.
library(mvmeta)
data <- data.frame(Input, p_male=Craft2003$gender)
metarg_RE <- summary(mvmeta(cbind(C1, C2, C3, C4, C5, C6) ~ p_male,
S = covars, data = data, method = "reml"))
metarg_REModel specification
In general, a multivariate meta-analysis specifies the model at within-study and between-study levels Wei and Higgins (2013). For the within-study level, let \(\hat{\boldsymbol\theta}_i\) denote a vector of \(p\) observed effect size in the \(i\)th study, which is assumed from a multivariate normal distribution:
\[{{\hat{\boldsymbol\theta}}_{i}}\sim\text{MVN(}{{\boldsymbol\theta}_{i}},{{\boldsymbol\Sigma}_{i}})\text{ with } {{\boldsymbol\Sigma}_{i}}=\left[ \begin{matrix} s_{i1}^{2} & {{\rho }_{w12}}{{s}_{i1}}{{s}_{i2}} & \cdots & {{\rho }_{w1p}}{{s}_{i1}}{{s}_{ip}} \\ {{\rho }_{w21}}{{s}_{i1}}{{s}_{i2}} & s_{i2}^{2} & \cdots & {{\rho }_{w2p}}{{s}_{i2}}{{s}_{ip}} \\ \vdots & \vdots & \ddots & \vdots \\ {{\rho }_{wp1}}{{s}_{i1}}{{s}_{ip}} & {{\rho }_{wp2}}{{s}_{i2}}{{s}_{ip}} & \cdots & s_{ip}^{2} \\ \end{matrix} \right], \] where \({\boldsymbol\theta}_{i}\) is the vector of underlying true effect sizes for study \(i\) and \({{\boldsymbol\Sigma}_{i}}\) is the within-study variance-covariance matrix, which is composed of the sampling variance of each effect size on the diagonal, denoted by \(s_{ij}^{2}\) \((j=1,\dots,p)\) for the \(j\)th effect size, and the within-study covariance of each pair of effect sizes on the off-diagonal that reflects within-study correlation, denoted by \({{\rho }_{wjk}}\) for the \(j\)th and \(k\)th effect sizes. Here, index \(i\) is omitted for \({{\rho }_{w..}}\) for the reason of simplicity. The assumption for \({\boldsymbol\theta}_{i}\) is a multivariate normal distribution that centers around the true average effect sizes, \(\boldsymbol\theta=(\theta_1,\theta_2,\dots,\theta_p)^T\), across studies:
\[{{\boldsymbol\theta}_{i}}\sim\text{MVN(}\boldsymbol\theta,\boldsymbol\Omega) \text{ with } \boldsymbol\Omega=\left[ \begin{matrix} \tau _{1}^{2} & {{\rho }_{b12}}{{\tau }_{1}}{{\tau }_{2}} & \cdots & {{\rho }_{b1p}}{{\tau }_{1}}{{\tau }_{p}} \\ {{\rho }_{b21}}{{\tau }_{1}}{{\tau }_{2}} & \tau _{2}^{2} & \cdots & {{\rho }_{b2p}}{{\tau }_{2}}{{\tau }_{p}} \\ \vdots & \vdots & \ddots & \vdots \\ {{\rho }_{bp1}}{{\tau }_{1}}{{\tau }_{p}} & {{\rho }_{bp2}}{{\tau }_{2}}{{\tau }_{p}} & \cdots & \tau _{p}^{2} \\ \end{matrix} \right], \] where \(\boldsymbol\Omega\) is the between-study variance-covariance matrix, which is composed of the between-study variance for each true effect size on the diagonal and between-study covariance for each pair of effect sizes on the off-diagonal that reflects between-study correlations \({\rho }_{b..}\). This model can be also writen as \({{\hat{\boldsymbol\theta}}_{i}}\sim\text{MVN(}{{\boldsymbol\theta}},{{\boldsymbol\Sigma}_{i}}+\boldsymbol\Omega)\). In the following sections, the notation \(\theta\) is replaced according to different types of effect sizes, such as \(r\) for correlation and \(\delta\) for standardized mean difference.
Correlation coefficients
Let \(r_{ist}\) denote the correlation coefficient that describes the relationship between variables \(s\) and \(t\). Following the notation by Lu (2023), Ahn et al. (2015) and Ingram Olkin (1976), we have
\[\text{var}({{r}_{ist}})={{(1-\rho _{ist}^{2})}^{2}}/{{n}_{i}}\]
for the variance of \(r_{ist}\) and the covariance between \(r_{ist}\) and \({r}_{iuv}\) is \[\begin{align*} \text{cov}({{r}_{ist}},{{r}_{iuv}})=&[.5{{\rho }_{ist}}{{\rho }_{iuv}}({{\rho }^{2}}_{isu}+{{\rho }^{2}}_{isv}+{{\rho }^{2}}_{itu}+{{\rho }^{2}}_{itv})+{{\rho }_{isu}}{{\rho }_{itv}}+{{\rho }_{isv}}{{\rho }_{itu}} \\ & -({{\rho }_{ist}}{{\rho }_{isu}}{{\rho }_{isv}}+{{\rho }_{its}}{{\rho }_{itu}}{{\rho }_{itv}}+{{\rho }_{ius}}{{\rho }_{iut}}{{\rho }_{iuv}}+{{\rho }_{ivs}}{{\rho }_{ivt}}{{\rho }_{ivu}})]/{{n}_{i}} \end{align*}\]
When the transformed Fisher’s \(z\)s are used, their variances and covariances are computed by
\[\text{var}({{z}_{ist}})=1/({{n}_{i}}-3)\]
\[\text{cov}({{z}_{ist}},{{z}_{iuv}})={{\sigma }_{ist,uv}}/\left[ (1-\rho _{ist}^{2})(1-\rho _{iuv}^{2}) \right]\]
Use the example of Cooper, Hedges, and Valentine (2019) on page 388 as an illustration:
> r <- matrix(c(-0.074, -0.127, 0.324, 0.523, -0.416, -0.414), 1)
> n <- 142
> computvcov <- r.vcov(n = n, corflat = r, method = "average")
> round(computvcov$list.rvcov[[1]], 4)
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0.0070 0.0036 -0.0025 -0.0005 0.0018 0.0009
[2,] 0.0036 0.0068 -0.0025 -0.0002 0.0008 0.0017
[3,] -0.0025 -0.0025 0.0056 0.0001 0.0000 -0.0003
[4,] -0.0005 -0.0002 0.0001 0.0037 -0.0013 -0.0013
[5,] 0.0018 0.0008 0.0000 -0.0013 0.0048 0.0022
[6,] 0.0009 0.0017 -0.0003 -0.0013 0.0022 0.0048
> round(computvcov$list.vcov[[1]], 4)
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0.0072 0.0041 -0.0030 -0.0007 0.0023 0.0012
[2,] 0.0041 0.0072 -0.0030 -0.0003 0.0011 0.0022
[3,] -0.0030 -0.0030 0.0072 0.0001 0.0000 -0.0004
[4,] -0.0007 -0.0003 0.0001 0.0072 -0.0023 -0.0023
[5,] 0.0023 0.0011 0.0000 -0.0023 0.0072 0.0036
[6,] 0.0012 0.0022 -0.0004 -0.0023 0.0036 0.0072The \(z\) transformed correlation coefficients are saved in the output vector zr. Note that for \(m\) outcomes, there are \(p=m\times (m-1)/2\) correlation coefficients. Since the \(p\) by \(p\) matrix is symmetric, there are \(p+(p-1)+(p-2)\dots +1=p(p+1)/2\) unique elements. It is more convenient to store these unique elements in a vector, so that if we have \(N\) studies, we could have a \(N\) by \(p(p+1)/2\) matrix that saves all the variances and covariances, which is named zcov as an output value and can be used for package mvmeta.
> data(Craft2003)
> corflat <- subset(Craft2003, select=C1:C6)
> computvocv <- r.vcov(n = Craft2003$N, corflat = corflat, method = "average")
> input <- computvocv$ef
> covars <- computvocv$matrix.vcov
> covars[1,]
[1] 0.0476190476 0.0003351688 0.0021381126 -0.0105790705 -0.0137617708
[6] -0.0011673589 0.0476190476 0.0039987417 0.0250656051 0.0023052534
[11] -0.0135408286 0.0476190476 0.0019637462 0.0251240397 -0.0104800258
[16] 0.0476190476 0.0058798781 -0.0017802532 0.0476190476 -0.0029485703
[21] 0.0476190476
> library(mvmeta)
> mvmeta_RE <- summary(mvmeta(cbind(C1, C2, C3, C4, C5, C6),
+ S = covars, data = input, method = "reml"))Standardized mean difference (SMD)
For the treatment group, let \(n_{jt}\), \(n_{kt}\) and \(n_{jkt}\) denote the numbers of participants who report outcome \(j\), outcome \(k\) and both outcome \(j\) and outcome \(k\). Similarly, denote \(n_{jc}\), \(n_{kc}\) and \(n_{jkc}\) for the control group. This notation is used for all the effect sizes for treatment comparison, including standardized mean difference, standardized mean difference (SMD), log odds ratio (logOR), log risk ratio (logRR), and risk difference (RD). Wei and Higgins (2013) derived the covariance between two effect sizes in terms of Hedges’ g, denoted by \(\delta_{j}\) and \(\delta_{k}\), as follows
\[\begin{align*} \text{cov}({\delta_{j}},{\delta_{k}})&= \rho\Big(\frac{n_{jkc}}{n_{jc}n_{kc}}+\frac{ n_{jkt}}{n_{jt}n_{kt}}\Big)+ \frac{k_{jk}}{k_jk_k} \rho^2 \delta _{j} \delta _{k}J(v_j)J(v_k)\sqrt{\Big(\frac{v_j}{v_j-2}-\frac{1}{{J(v_j)}^2}\Big)\Big(\frac{v_k}{v_k-2}-\frac{1}{{J(v_k)}^2}\Big)},\\ \text{ where }k_k&=\frac{2n_{kt}+2n_{kc}-4}{(n_{kc}+n_{kt}-2)^2},\\ k_j&=\frac{2n_{jt}+2n_{jc}-4}{(n_{jc}+n_{jt}-2)^2},\\ k_{jk}&=\frac{2}{(n_{jc}+n_{jt}-2)(n_{kc}+n_{kt}-2)}\Big(\frac{n_{jt}n_{kt}}{n_{jt}+n_{kt}-1}+\frac{n_{jc}n_{kc}}{n_{jc}+n_{kc}-1}-2\Big),\\ \end{align*}\]
and \({\delta}_{j}\) and \({\delta}_{k}\) are the observed SMD for outcome \(j\) and \(k\). As a comparison, we also provide the formula in I. Olkin and Gleser (2009) for SMD as cohan’s \(d\), which is defined as
\[\text{cov}^{d}({\delta_{j}},{\delta_{k}})=\frac{(n_{{t}}+n_{{c}}){{\rho }_{jk}}}{n_{{t}}n_{{c}}}+\frac{\delta _{j}^{{}}\delta _{k}^{{}}\rho _{jk}^{2}}{2(n_{{t}}+n_{{c}})},\]
library(metavcov)
data(Geeganage2010)
r12 <- 0.71
r.Gee <- lapply(1:nrow(Geeganage2010), function(i){matrix(c(1, r12, r12, 1), 2, 2)})
computvocv <- smd.vcov(nt = subset(Geeganage2010, select = c(nt_SBP, nt_DBP)),
covars <- computvocv$matrix.vcov
head(covars)
[,1] [,2] [,3]
[1,] 0.15560955 0.11051462 0.15591453
[2,] 0.18256182 0.12959901 0.18254277
[3,] 0.03190808 0.02264927 0.03198210
[4,] 0.03115906 0.02212545 0.03119080
[5,] 0.01965510 0.01395547 0.01967717
[6,] 0.26813782 0.18910349 0.26680797
covars <- computvocv$matrix.dvcov
head(covars)
[,1] [,2] [,3]
[1,] 0.15565024 0.11056752 0.15618509
[2,] 0.18257730 0.12959610 0.18254492
[3,] 0.03200824 0.02271517 0.03215273
[4,] 0.03117474 0.02213897 0.03123674
[5,] 0.01965512 0.01395583 0.01969852
[6,] 0.26896403 0.18897441 0.26688733
Cite this website as
M. Lu. 2021. “metavcov vignette.” https://luminwin.github.io/metavcov/articles/intro.html.
@misc{LumetavcovV,
author = "Min Lu",
title = {{metavcov} vignette},
year = {2021},
url = {https://luminwin.github.io/metavcov/articles/intro.html},
howpublished = "\url{https://luminwin.github.io/metavcov/articles/intro.html}",
note = "[accessed date]"
}
@ARTICLE{LuFrontier2023,
AUTHOR = {Lu, Min},
TITLE = {Computing Within-Study Covariances, Data Visualization and Missing Data Solutions for Multivariate Meta-Analysis with {metavcov}},
JOURNAL = {Frontiers in Psychology},
VOLUME = {14},
YEAR = {2023},
NUMBER = {1185012},
URL = {https://www.frontiersin.org/articles/10.3389/fpsyg.2023.1185012},
DOI = {10.3389/fpsyg.2023.1185012}
}