Computing Variance-Covariance Matrices for Standardized Mean Differences — smd.vcov • Computing Variances and Covariances, Visualization and Missing Data Solution for Multivariate Meta-Analysis with metavcov

The function lgOR.vcov computes effect sizes and variance-covariance matrix for multivariate meta-analysis when the effect sizes of interest are all measured by standardized mean difference. See mix.vcov for effect sizes of the same or different types.

smd.vcov(nt, nc, d, r, n_rt = NA, n_rc = NA, name = NULL)

Arguments

nt	A $N \times p$ matrix storing sample sizes in the treatment group reporting the $p$ outcomes. `nt[i,j]` is the sample size from study $i$ reporting outcome $j$ .
nc	A matrix defined in a similar way as `nt` for the control group.
d	A $N \times p$ matrix or data frame with standard mean differences (SMD) from the $N$ studies. `d[i,j]` is the value from study $i$ for outcome $j$ .
r	A $N$ -dimensional list of $p \times p$ correlation matrices for the $p$ outcomes from the $N$ studies. `r[[k]][i,j]` is the correlation coefficient between outcome $i$ and outcome $j$ from study $k$ .
n_rt	A $N$ -dimensional list of $p \times p$ matrices storing sample sizes in the treatment group reporting pairwise outcomes in the off-diagonal elements. `n_rt[[k]][i,j]` is the sample size reporting both outcome $i$ and outcome $j$ from study $k$ . Diagonal elements of these matrices are discarded. The default value is `NA`, which means that the smaller sample size reporting the corresponding two outcomes is imputed: i.e. `n_rt[[k]][i,j]=min(nt[k,i],nt[k,j])`.
n_rc	A list defined in a similar way as `n_rt` for the control group.
name	Names for the outcomes.

Author

Min Lu

Value

ef	A $N \times p$ data frame that transforms the input argument `d` into Hedges's g (Wei and Higgins, 2013).
list.vcov	A $N$ -dimensional list of $p(p+1)/2 \times p(p+1)/2$ variance-covariance matrices for Hedges's g (Wei and Higgins, 2013).
matrix.vcov	A $N \times p(p+1)/2$ whose rows are computed variance-covariance vectors for Hedges's g (Wei and Higgins, 2013).
list.dvcov	A $N$ -dimensional list of $p(p+1)/2 \times p(p+1)/2$ variance-covariance matrices for SMD (Olkin and Gleser, 2009).
matrix.dvcov	A $N \times p(p+1)/2$ matrix whose rows are computed variance-covariance vectors for SMD (Olkin and Gleser, 2009).

References

Ahn, S., Lu, M., Lefevor, G.T., Fedewa, A. & Celimli, S. (2016). Application of meta-analysis in sport and exercise science. In N. Ntoumanis, & N. Myers (Eds.), An Introduction to Intermediate and Advanced Statistical Analyses for Sport and Exercise Scientists (pp.233-253). Hoboken, NJ: John Wiley and Sons, Ltd.

Wei, Y. & Higgins, J. (2013). Estimating within study covariances in multivariate meta-analysis with multiple outcomes. Statistics in Medicine, 32(7), 119-1205.

Olkin, I. & Gleser, L. (2009). Stochastically dependent effect sizes. In H. Cooper, L. V. Hedges, & J. C. Valentine (Eds.), The handbook of research synthesis and meta-analysis (pp. 357-376). New York: Russel Sage Foundation.

Examples

######################################################
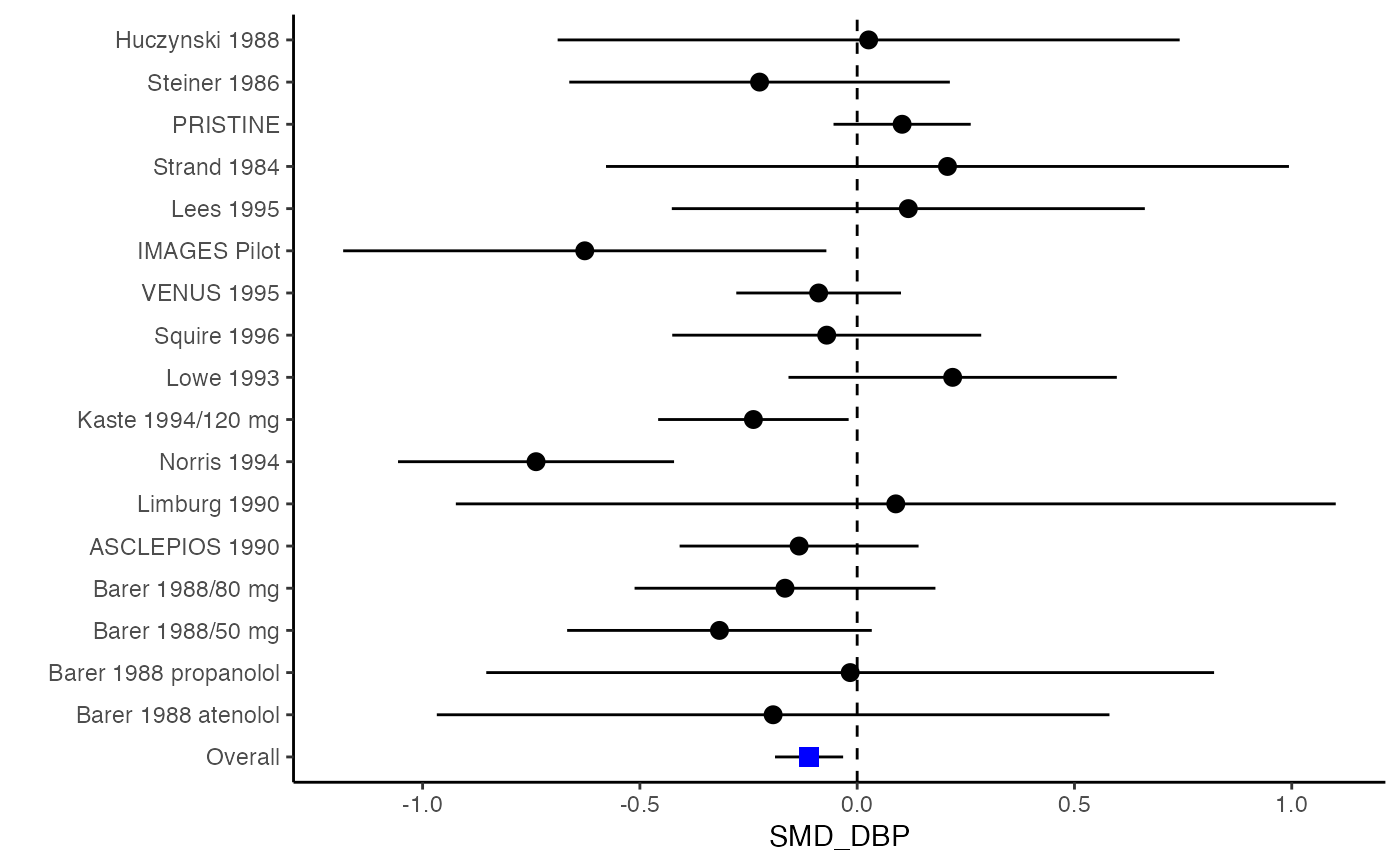
# Example: Geeganage2010 data
# Preparing covarianceS for multivariate meta-analysis
######################################################
data(Geeganage2010)
## set the correlation coefficients list r
r12 <- 0.71
r.Gee <- lapply(1:nrow(Geeganage2010), function(i){matrix(c(1, r12, r12, 1), 2, 2)})

computvcov <- smd.vcov(nt = subset(Geeganage2010, select = c(nt_SBP, nt_DBP)),
               nc = subset(Geeganage2010, select = c(nc_SBP, nc_DBP)),
               d = subset(Geeganage2010, select = c(SMD_SBP, SMD_DBP)), r = r.Gee,
               name = c("SMD_SBP", "SMD_DBP"))
# name variance-covariance matrix as S
S <- computvcov$matrix.vcov
## fixed-effect model
y <- computvcov$ef
MMA_FE <- summary(metafixed(y = y, Slist = computvcov$list.vcov))
#######################################################################
# Running random-effects model using package "mvmeta" or "metaSEM"
#######################################################################
# Restricted maximum likelihood (REML) estimator from the mvmeta package
#library(mvmeta)
#mvmeta_RE <- summary(mvmeta(cbind(SMD_SBP, SMD_DBP),
#                     S = S,
#                     data = y,
#                     method = "reml"))
#mvmeta_RE

# maximum likelihood estimators from the metaSEM package
# library(metaSEM)
# metaSEM_RE <- summary(meta(y = y, v = S))
# metaSEM_RE
##############################################################
# Plotting the result:
##############################################################
obj <- MMA_FE
# obj <- mvmeta_RE
# obj <- metaSEM_RE
# pdf("CI.pdf", width = 4, height = 7)
plotCI(y = computvcov$ef, v = computvcov$list.vcov,
        name.y = NULL, name.study = Geeganage2010$studyID,
        y.all = obj$coefficients[,1],
        y.all.se = obj$coefficients[,2])
#> $`Plotting SMD_SBP`
#> 
#> $`Plotting SMD_DBP`
#> 
# dev.off()